Dealing with Imbalanced Datasets

This repository serves as an illustration of how this problem may appear in a real-world scenario and how to deal with it.
Imagine the CFO of your organization comes to you complaining about how the recent uprise of e-commerce after the Covid outbreak has increased the risk of credit card fraud. As a Data Scientist, you start gathering data from the company’s financial records and start building a baseline model that can show the potential of this task. After a couple of days of work, you have a model that predicts fraudulent transactions with 99.9% precision. You run to the CFO to inform her/him of the good news but you get reprimanded as your model is deemed useless. What happened?
The problem is that, as the dataset is highly imbalanced, you model is predicting that every one of the transactions is legit, so it’s unable to detect one single fraudulent transaction. This is a common problem in many industries, and it’s important to know how to deal with it.
What is an imbalanced dataset?
An imbalanced dataset is a dataset where the number of observations in one class is significantly higher than the number of observations in the other classes. In the example above, the number of fraudulent transactions is much lower than the number of legit transactions, with a proportion of 1 fraudulent transaction by at least 999 legit ones. This is a common problem in many industries, such as fraud detection, medical diagnosis, and mechanical engineering, where defective parts are much rare than correct ones.
Imbalanced datasets cause problems in Machine Learning as models are focused on maximizing the accuracy of the ensemble of predictions. In the example above, the model will predict that every transaction is legit, and it will be right 99.9% of the time. This is a problem because the model will not able to detect any of the fraudulent transactions, proving itself useless for the task at hand.
How to deal with imbalanced datasets
In the academic literature several methods are approached to deal with this particular problem. As with any other problem in Machine Learning, there is no such thing as a free lunch, and each method has its own pros and cons. In this post, I will cover the most common methods to deal with imbalanced datasets, and I will show how to implement them in Python.
Dataset resampling
One of the main ways to deal with imbalanced datasets is to directly resample them. The 2 main ways to perform this operation are Oversampling, which consists in adding more observations to the minority class, and Undersampling, which consists in removing observations from the majority class. In the example above, we could add more fraudulent transactions to the dataset, or we could remove legit transactions from the dataset.
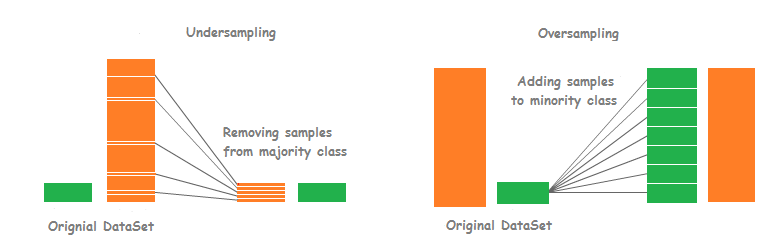
Although we could use random approaches to perform both over and under sampling, to perform this operations we have more advanced methods such as SMOTE or NearMiss, both based on Nearest Neighbors models, for repectively over and under sampling. These methods are implemented in the imbalanced-learn Python library are easy enough to implement:
from imblearn.under_sampling import NearMiss
from imblearn.over_sampling import SMOTE
# Change between the desired resampling method
resampler = NearMiss()
# resampler = SMOTE()
X_resampled, y_resampled = resampler.fit_resample(X, y)
This kind of transformers work quite fine out-of-the-box, but some parameters we may want to tune are the number of neighbors to consider when resampling, and the sampling proportions. In the example above, we are using the default parameters, but we could tune them to get better results.
It’s extremely important not to resample the test partition of the dataset, as we want it to be as close as possible to the real world scenario, when the classes will keep their natural imbalance.
Metric Selection
Another way to deal with imbalanced datasets is to select a metric that is more focused on the minority class. In the example above, we could use the F1 score instead of the accuracy, as it is more focused on the minority class. This way, we will be able to detect the fraudulent transactions, even if we are not able to detect all of them.
As with many other metrics, the F1 score is implemented in the scikit-learn library:
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import f1_score
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=5000, n_features=2, n_informative=2,
n_redundant=0, n_repeated=0, n_classes=3,
n_clusters_per_class=1,
weights=[0.01, 0.05, 0.94],
class_sep=0.8, random_state=0)
clf = LogisticRegression()
clf.fit(X, y)
y_pred = clf.predict(X)
print(f"F1 obtained: {f1_score(y, y_pred, average='macro'}")
If we are instead using PyTorch, we can use the F1 score implemented in the torchmetrics library:
from torchmetrics import F1Score
import torch
from torch.utils.data import DataLoader
from torch import nn
from torch import optim
from sklearn.datasets import make_classification
class Net(nn.Module):
"""
Simple neural network with 2 hidden layers
"""
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(2, 10)
self.fc2 = nn.Linear(10, 3)
def forward(self, x):
x = self.fc1(x)
x = nn.functional.relu(x)
x = self.fc2(x)
return x
X, y = make_classification(n_samples=5000, n_features=2, n_informative=2,
n_redundant=0, n_repeated=0, n_classes=3,
n_clusters_per_class=1,
weights=[0.01, 0.05, 0.94],
class_sep=0.8, random_state=0)
X = torch.from_numpy(X).float()
y = torch.from_numpy(y).long()
model = Net()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
f1 = F1Score(task="multiclass", num_classes=3, average='macro')
with tqdm(total=100) as pbar:
for epoch in range(100):
for x, y in DataLoader(list(zip(X, y)), batch_size=32):
optimizer.zero_grad()
y_pred = model(x)
loss = criterion(y_pred, y)
loss.backward()
optimizer.step()
pbar.update(1)
pbar.set_description(f"Loss: {loss.item():.4f} - F1: {f1(y_pred, y):.4f}")
print(f"F1 obtained: {f1(y_pred, y)}")
Some other useful metrics to consider here are the Precision-Recall curve and the ROC curve, so feel free to check them out while building and evaluating your models.
Cost-sensitive learning
Another way to deal with imbalanced datasets is to use cost-sensitive learning. In this approach, we assign a cost to each class, and we use this cost to weight the loss function of the model. This way, the model will be more focused on minimizing the loss of the minority class, and it will be less focused on minimizing the loss of the majority class. This approach is implemented in the scikit-learn library with the class_weight parameter:
# The code would be the same as in the previous section but with the following change
clf = LogisticRegression(class_weight={0: 0.01, 1: 0.05, 2: 0.94})
A similar implementation can take place in PyTorch with the torch.nn.CrossEntropyLoss class:
# The code would be the same as in the previous section but with the following change
criterion = nn.CrossEntropyLoss(weight=torch.tensor([0.01, 0.05, 0.94]))
Do nothing
Yes! You read that right. Sometimes, the best way to deal with imbalanced datasets is to do nothing. In some cases, the model will be able to detect the minority class even if it is not able to detect all of them. With neural networks this approach has gained some popularity recently due to their predictive power, so do not be afraid to try it out.
Final remarks
Imbalanced datasets are one of the most common problems on modern applications of Machine Learning. It’s difficult to stumble upon a dataset that is perfectly balanced in a production environment. In this article, we have seen some of the most common approaches to deal with imbalance, and we have seen how to implement them in Python. The key takeaway from this article is that there is no one-size-fits-all solution to this problem. You will have to validate several approaches with the test set against imbalance robust metrics such as F1 or AUC.
I hope that you have found this article useful, and that you will be able to use these techniques in your future projects. See you soon!